PhysicsBowl 2016 Q27

PhysicsBowl Home Page

PhysicsBowl 2016

27) In this question, we know the ƒ frequency tuning fork produces a third harmonic standing wave for a tube covered on one end. Now, we need to find the frequency needed for the fourth harmonic in terms of ƒ.

Let's start by looking at a tube of length L covered on one side. We can come up with this relation for lambda, the wavelength.

Where L is length, λ is wavelength, and n is the harmonic number

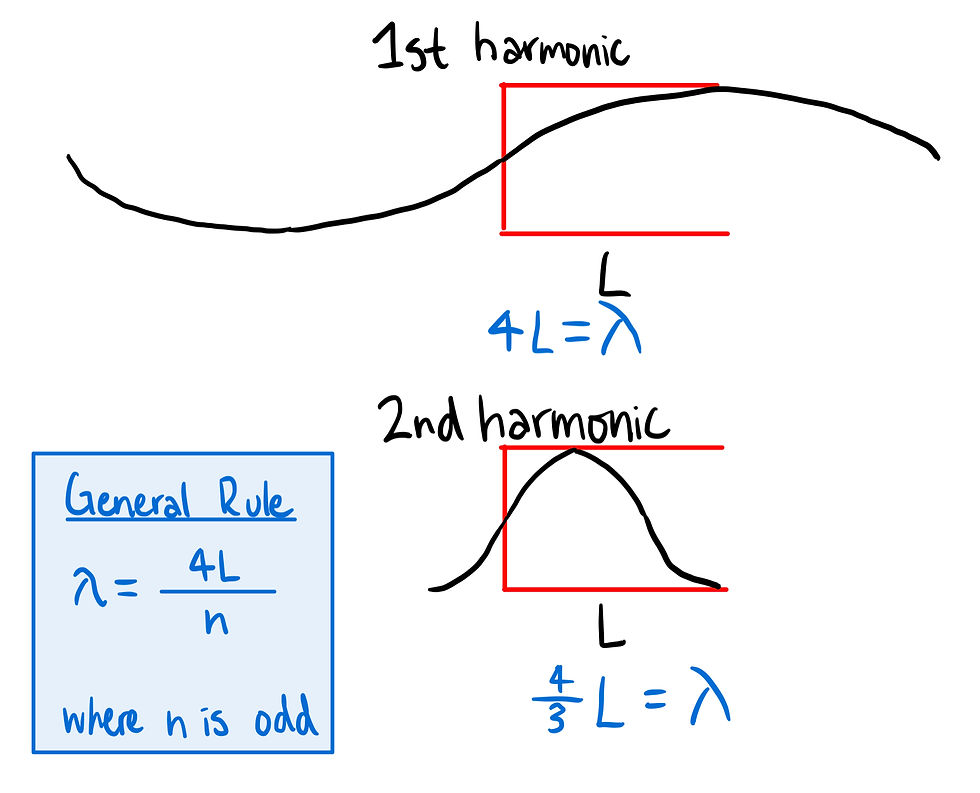
Note that n must be odd in a tube with one side covered. This means our 2nd harmonic actually corresponds to n=3, 3rd to n=5, 4th to n=7...

Using the general rule we have found and the wave equation, we can find an equation for the frequency of this wave.

Where L is length, λ is wavelength, n is the harmonic number, v is wave velocity, and ƒ is frequency

Velocity(v) and tube length(L) will be constant between both situations, so n is our only variable in this situation.

At this point, we know that the frequency at the 3rd harmonic (n=5) is ƒ. We just need to solve for the frequency at the 4th harmonic (n=7) in terms of ƒ.

Where n is the harmonic number, ƒ is frequency, v is wave velocity, and L is length

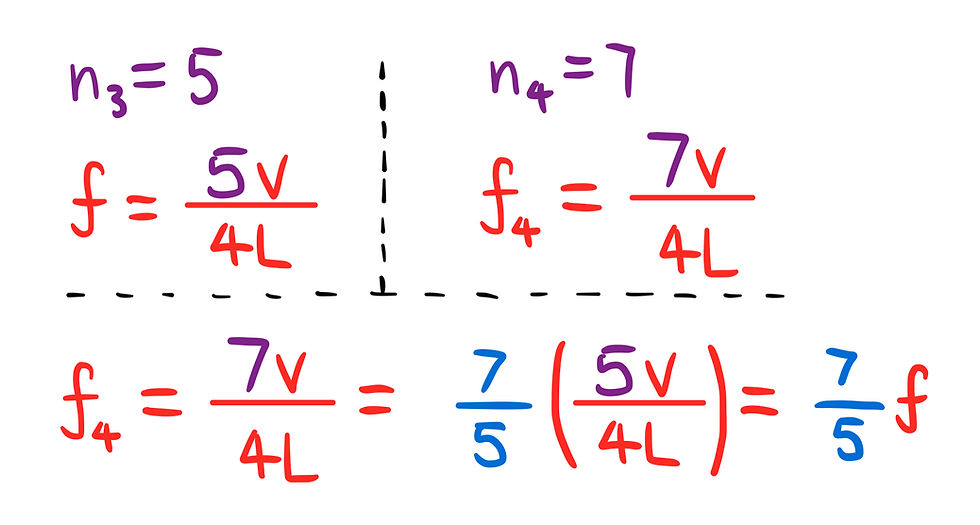
Answer: D