48) The problem gives us a situation where we have a simple circuit wired in series. We want to find how the resistance, current, and power would change if we were to add a second resistor to the circuit.
Since we are dealing with a series circuit, we need to make sure to compare with equations used for series. We should start with resistance because it is the simplest.
Since total resistance is just a sum of the resistance from all resistors, when we add another resistor, the total resistance will increase.
Now that we know the resistance will increase, we can take a look at the current.
We have a relation between resistance and current, but we can simplify it further. We can treat the voltage as a constant because the battery is not changing.
This shows the inverse relationship between resistance and current. As the resistance increases, the current decreases.
Lastly, we need to take a look at the power.
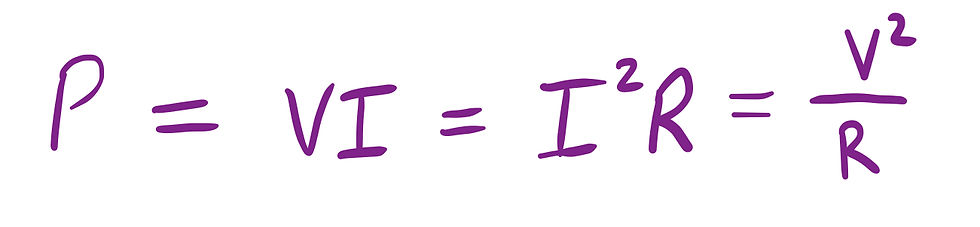
There are multiple ways to calculate the power, but since both current(I) and resistance(R) are changing, it will be easiest to choose one of the formulas that have one or the other. In the same manner, voltage is constant, so we can either take the first or the third one to make it easiest for us.
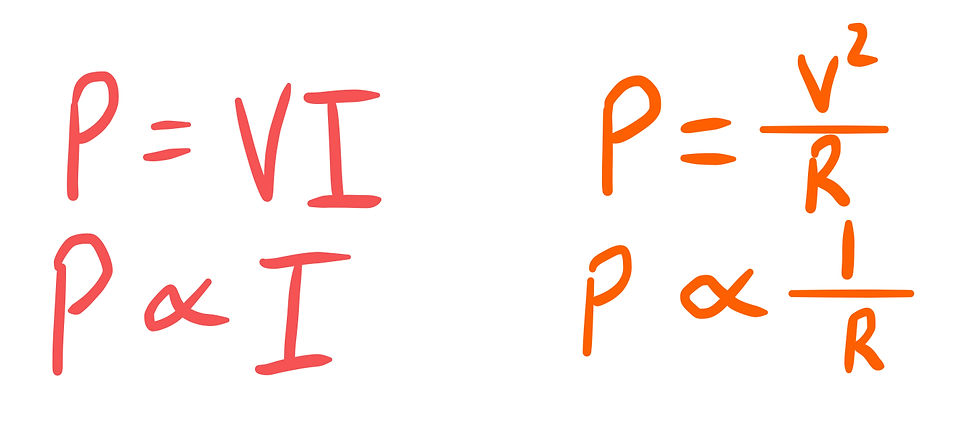
Looking at the red relation, we can tell that as the current(I) decreases, the power(P) will decrease as well. To confirm this answer, we can additionally look at the orange relation, which tells us that as the resistance(R) increases, the power(P) should decrease.
Answer: D
Comments