Barron's 2nd Edition PT1 Q31

Barron's Book

31) This question, a lot like question 30, asks us to find the speed needed at the top of the loop to continue in circular motion. Again, we would set the centripetal force to the net force in the y-direction.

Where F[c] is centripetal force, m is mass, v is speed, r is radius of circular path, and F[Net] is the net force

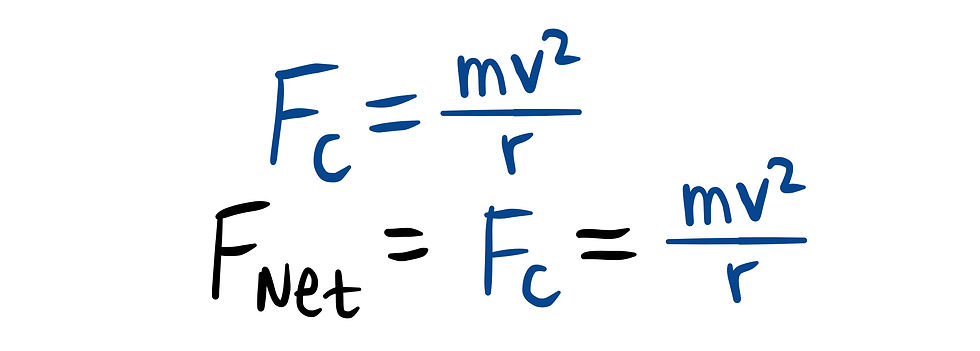
Next, we would continue by drawing a force diagram for all forces at the top of the loop. It is important to know that in order for the ball to travel through the top point of the circle with minimum speed, there will be no tension at the top.

Where F[g] is gravitational force

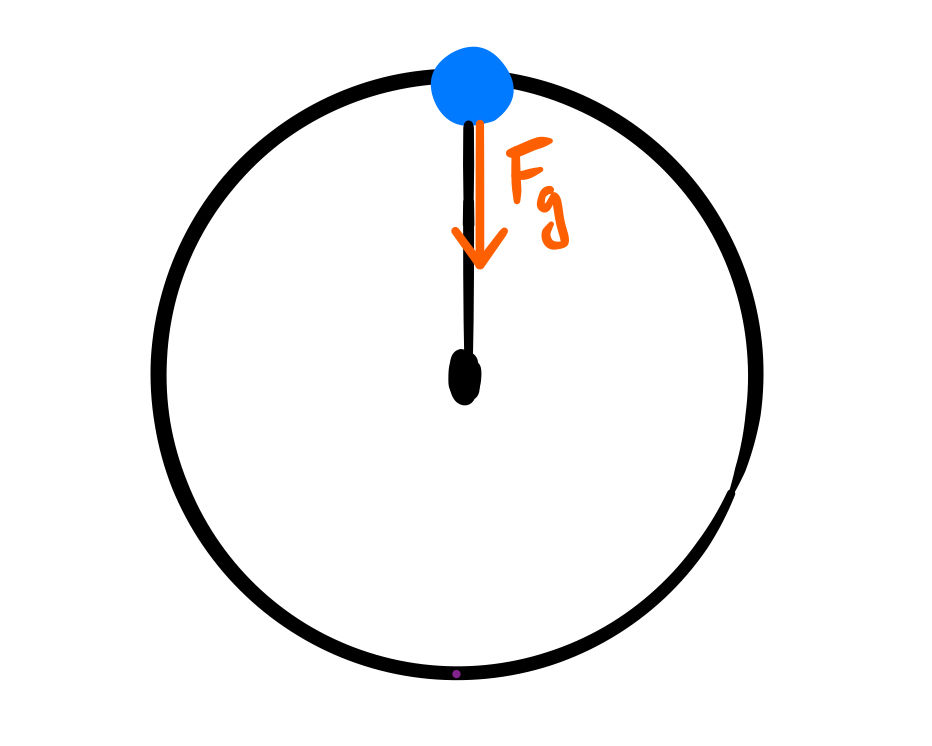
Gravity is the only force acting on the mass, so we consider it our net force. We can solve for the velocity now.

Where F[Net] is net force, F[c] is centripetal fore, F[g] is gravitational force, m is mass, g is acceleration of gravity, v is speed, and r is radius of circular path

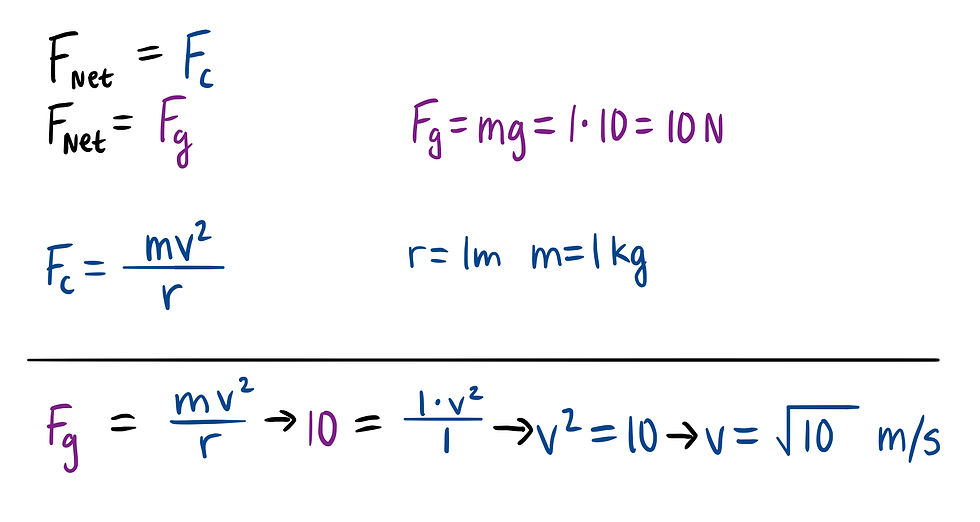
Answer: C