Barron's 2nd Edition PT1 Q34

Barron's Book

34) This question poses us with a situation where a car is kept in circular motion by the friction between it and the road. We need to find out what happens to the maximum speed if the mass of the car is doubled. Let’s start with the free body diagram.

Where N is normal force, f is friction force, and F[g] is gravitational force

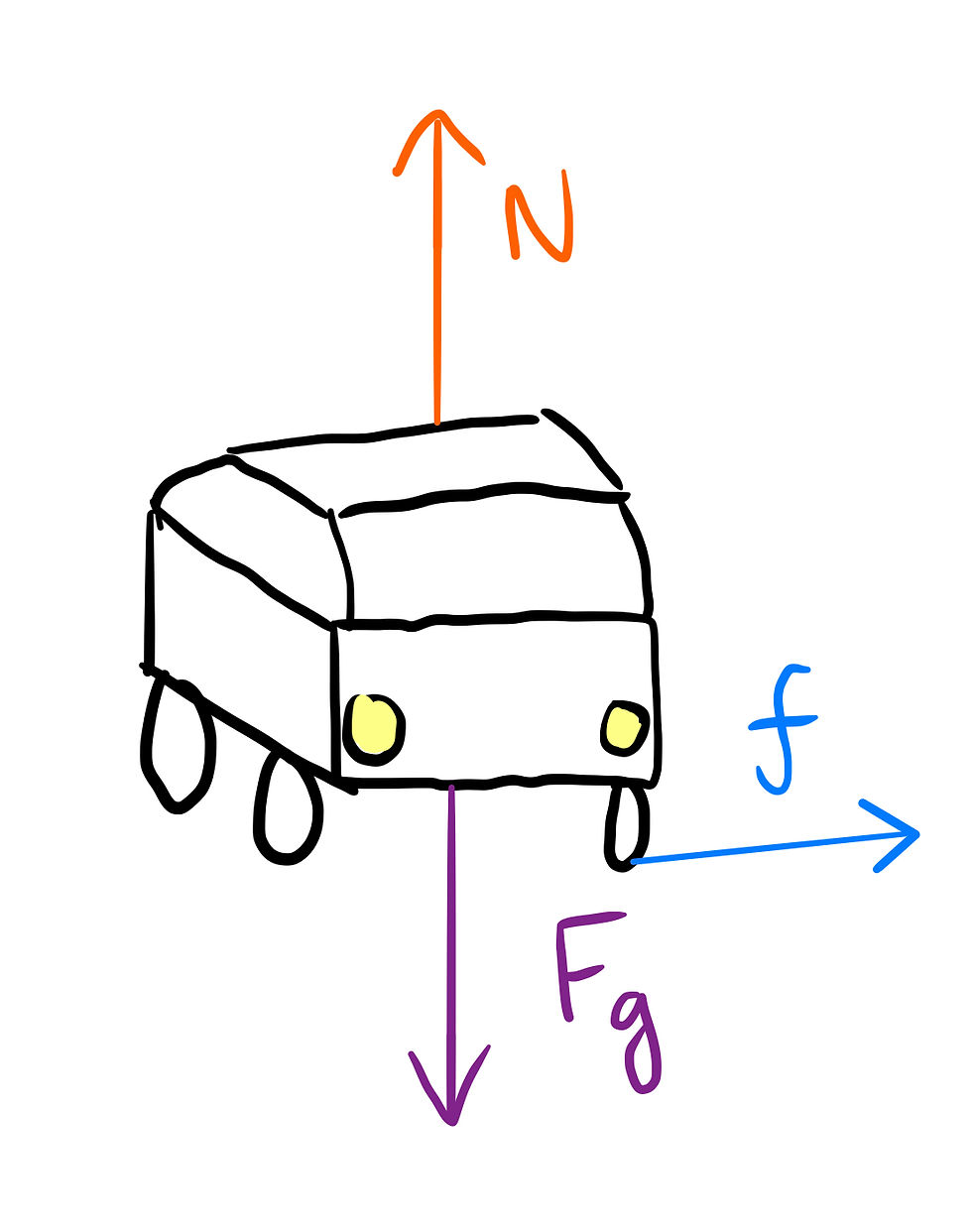
Since the car travels in circular motion, we can equate the centripetal force to the net force in the x-direction.

Where F[c] is centripetal force, F[Net, x] is the net force in the x-direction, m is mass, v is speed, r is radius of circular path, and f is friction force

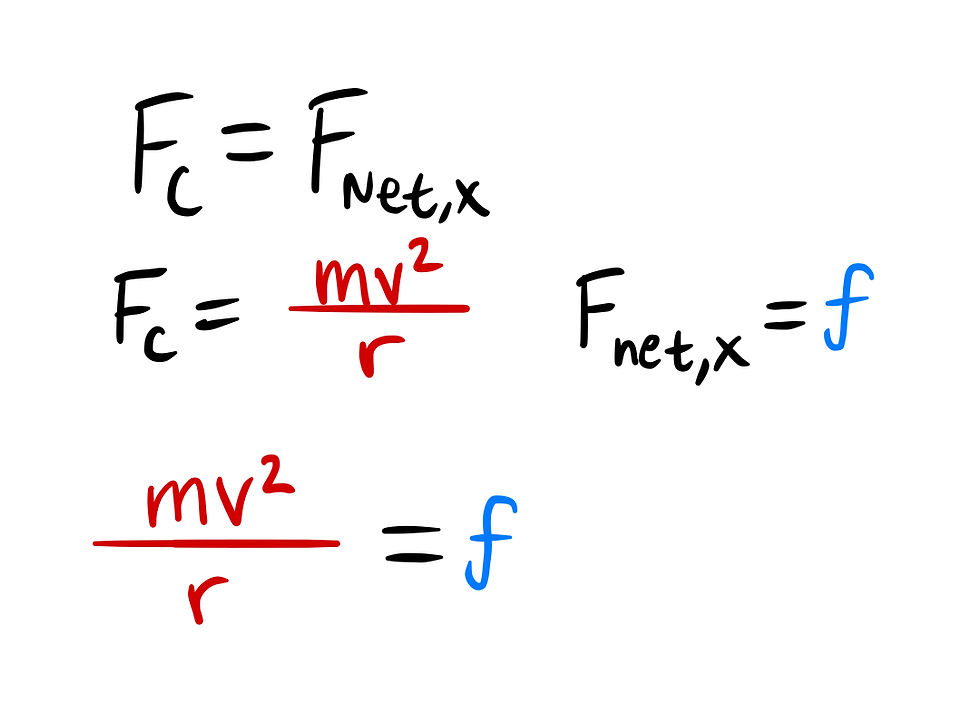
Great! We have an equation relating mass to velocity, but the friction can be simplified further. Friction is always the normal force multiplied by the coefficient of friction.

Where f is friction, N is normal, mu is coefficient of friction, F[Net, y] is the net force in the y-direction, F[g] is gravitational force, m is mass, g is acceleration due to gravity, v is speed and r is radius of circular path

Now, when we look at the fully simplified equation, we can see that the mass of the car will not affect the maximum speed. This means if the mass is doubled the maximum speed will stay at v.

If we had stopped at the previous step without simplifying the friction force, we would’ve got the wrong answer.

Answer: C