23) This question requires us to consider the types of mechanical energy in this spring system. We are asked to consider which types of energy will increase.
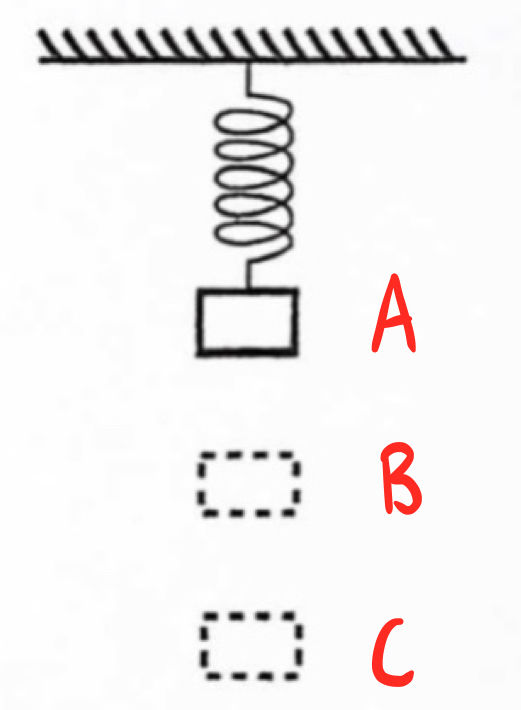
The spring starts at point A. We want to find the quantity that increases as the object moves from A to B.
We can start with elastic potential energy from the spring.
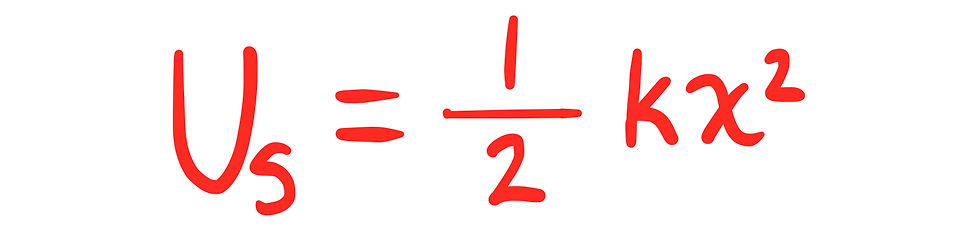
The problem states that the spring starts compressed before being released. That means the hanging mass moves towards the equilibrium position just after being released. Since the distance from the equilibrium decreases, the elastic potential energy will decrease when the mass is released.
Next, we can take a look at how the gravitational potential energy is affected.
Because of the combination of gravitational force and the spring's restoring force, we can tell that the object will move down. Since gravitational potential energy is related to the height, as the mass moves to a lower height, U[g] will decrease.
Finally, we need to consider kinetic energy.
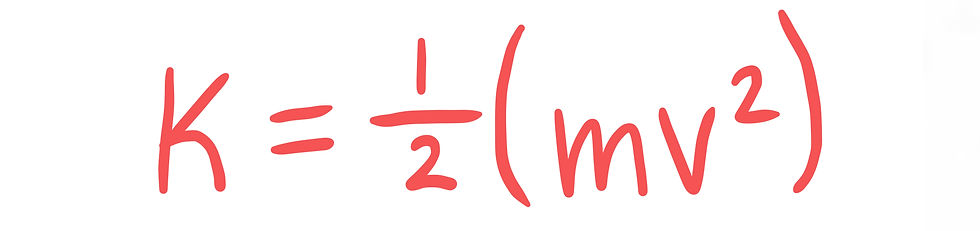
One way to think of this is with force. As mentioned above, when the mass is just released, the gravitational force and the spring's restoring force both point downward. That means the acceleration will cause the speed to increase; as the speed increases, the kinetic energy increases as well.
Here's is another way to think of the system's kinetic energy.
We can also consider the kinetic energy with work. We know that, for a conservative system, the change in kinetic energy is equal to the negative change in potential energy. So this means that since we proved that both the elastic and gravitational potential energy will decrease, we can immediately tell that the kinetic energy will increase.
Answer: C
コメント