37) This question asks us to approximate Earth's angular momentum of its orbit around the Sun. It is important to notice that we want to determine Earth's angular momentum around the Sun and not around its own axis. This mistake could vary the answer greatly.
We can express angular momentum as the product of the moment of inertia and angular speed.
We can approximate Earth to be a sphere of uniform density. This makes the moment of inertia simple to solve for. We know the moment of inertia of a sphere about its center, however we are considering Earth's motion around the Sun. Thus, we can use the parallel axis theorem to account for this.
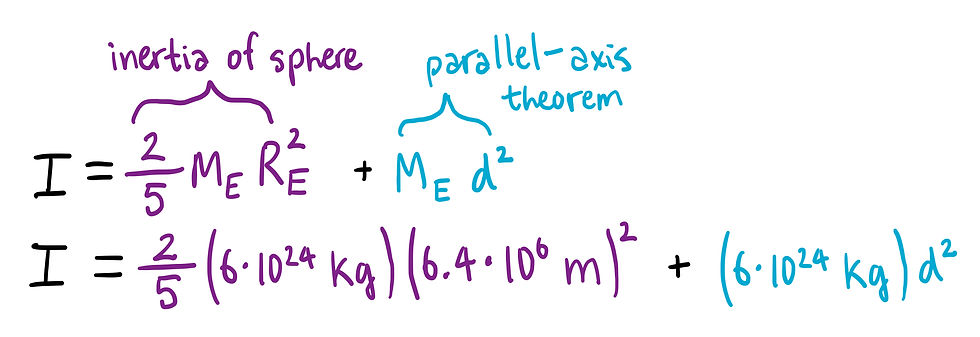
Usually, with the parallel-axis theorem, d would measure the distance between the center of mass of the sphere, and the axis of rotation. Since the Earth's orbit around the Sun is nearly circular with the Sun close to the center, we will approximate d as the distance between the Sun and the Earth. We can approximate this distance as the distance light travels in 10 minutes.
Next, we need to determine the angular speed of the Earth around the Sun. We know that the Earth completes one full orbit each year. This means it covers 2π radians in one year. From this information, we can find the average angular speed of the Earth.
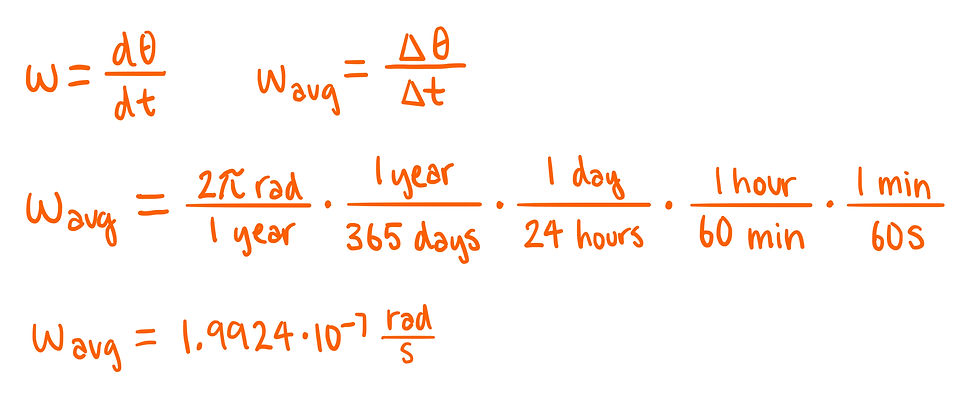
Finally, we have both the moment of inertia and the angular speed of Earth. We can finally, solve for angular momentum.
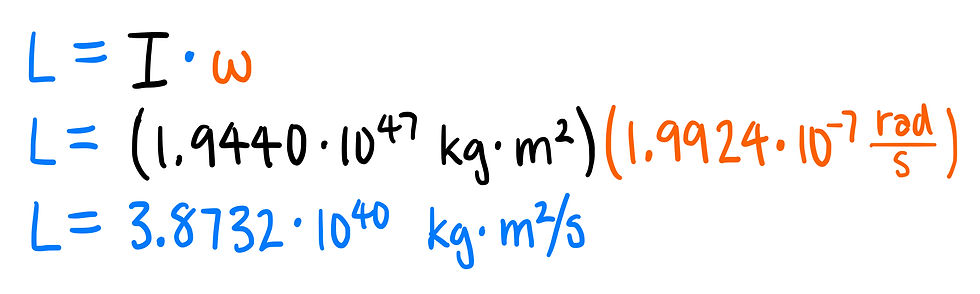
Answer: B
Comments