top of page
  • Writer's picturekeshprad

PhysicsBowl 2017 Q38


38) In this question we have a bucket spinning vertically in centripetal motion. We know that at the top of the motion, the bucket moves just fast enough such that the 2kg block inside the bucket stays put. We need to find the normal force when the bucket makes a 30° angle with the vertical.


Let's draw a free-body diagram of the bucket when it is at the top of the path.

Where F[g] is gravitational force, m is mass, and a is acceleration due to gravity

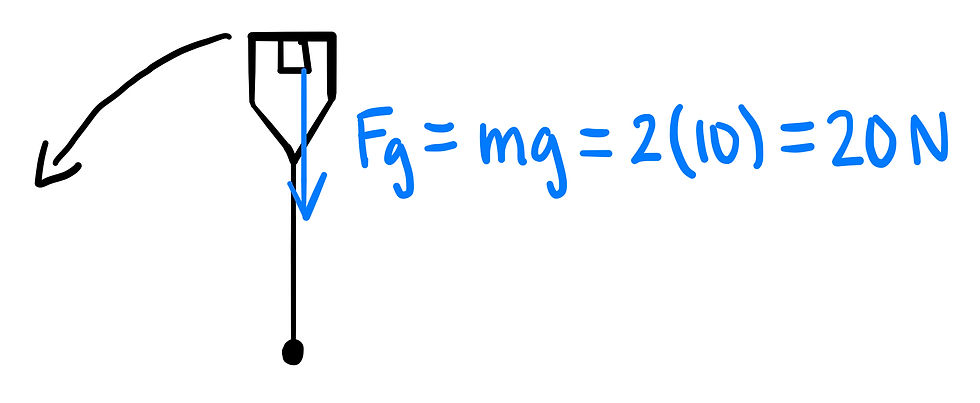
Since gravity is the only force, and the net force acting towards the center of the motion, we can equate this to our centripetal force to solve for the velocity at this point.

Where F[c] is centripetal force, F[g] is gravitational force, m is mass, v is velocity, and L is radius of circular path

Next, we can set up an equation for the centripetal force when the bucket is at 30°. Let's start with the force diagram.

Where F[g] is gravitational force, and N is normal force

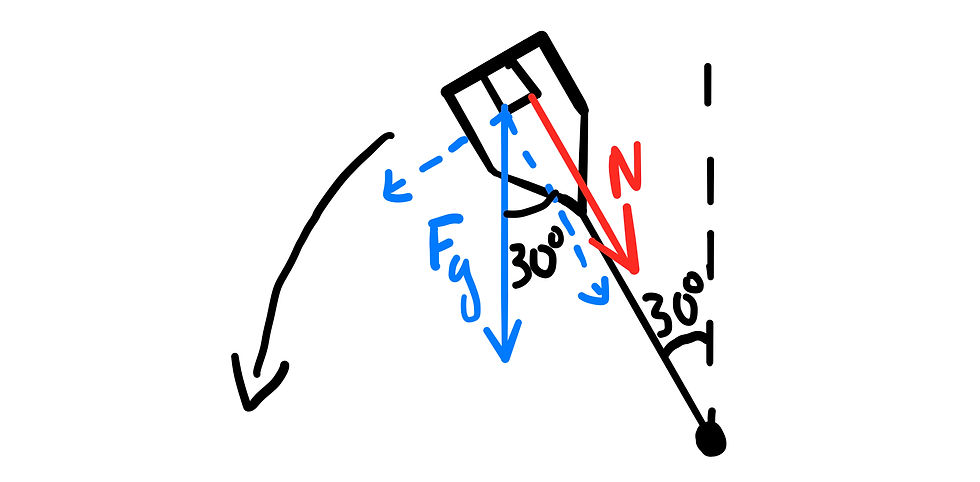
Remember that centripetal force describes the net force towards the center of the object's motion. This means only one component of gravity will be included.

Where F[c] is centripetal force, F[g] is gravitational force, θ is the given angle, N is normal force, m is mass, v is velocity, L is radius of circular path, and g is acceleration due to gravity

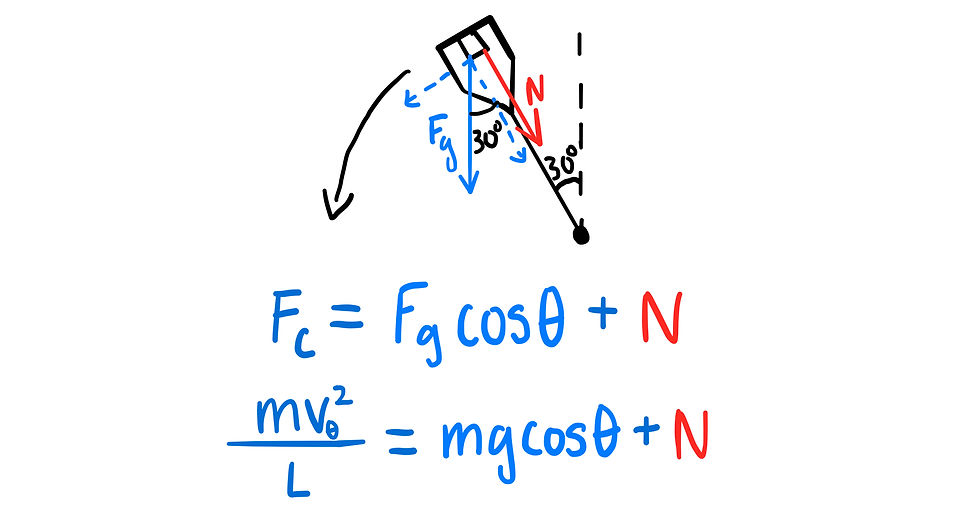
At this point, all we need to solve for v[θ], the speed of the block when the bucket makes a 30° angle with the vertical. We can use the conservation of energy to determine v[θ].

Where m is mass, g is acceleration due to gravity, L is radius of circular path, v is velocity, and θ is the given angle

Now, we can go back to our centripetal force equation and solve for N.

Where N is normal force, m is mass, v is velocity, L is radius of circular path, g is acceleration due to gravity, and θ is the given angle

Answer: A

Comments

bottom of page