24) This question asks us to find the maximum height of the object given its initial conditions. This is the setup we are given. In order to find the maximum height, we can either use energy or kinematics. I'll solve through both for this problem.
Energy: Using the conservation of mechanical energy, we know that the sum of the kinetic and potential energy at the ground, will be equal to the sum of the kinetic and potential energy at max height.
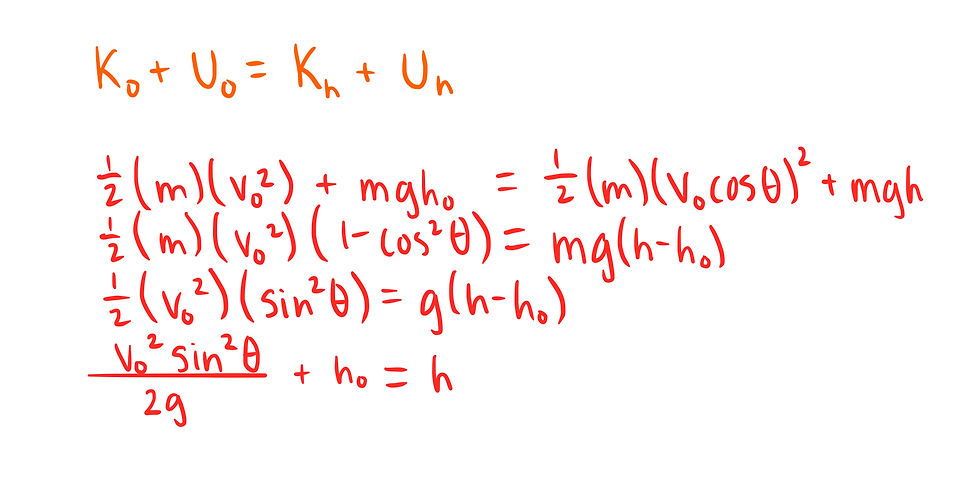
Recall that at max height, there is no vertical component of the velocity, so our speed is v*cos(θ).
Starting with the general form of the conservation of energy, we were able to come up with an equation for the max height. Finally, plugging in our known values, we will come up with the answer.
Kinematics: We can also solve this question using kinematics. Since we only care about the maximum height, let's consider only vertical components of the motion.
The vertical component of the initial velocity will be v*sin(θ). We also know that the vertical component of our velocity at the maximum height will be 0. the only force acting on the object is gravity, so the vertical component of acceleration is -10 m/s^2.
When we solve this kinematic equation for h, we end with this equation. You might notice that this is the exact same equation we came up with while using the conservation of energy!
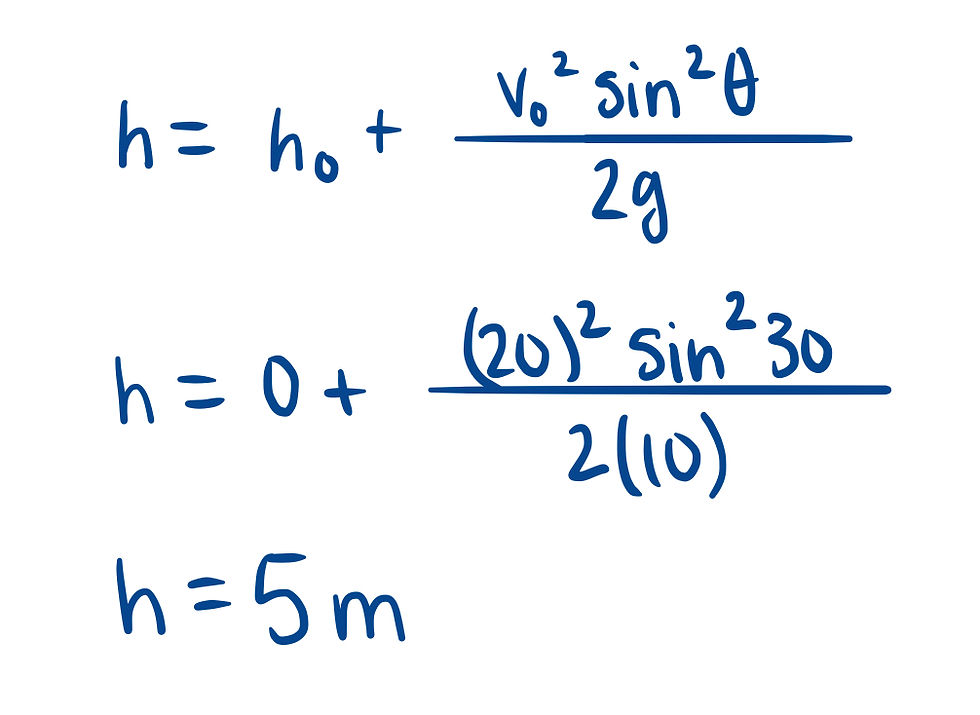
Whether we use the conservation of energy or kinematics, we will come up with the same answer for the maximum height.
Answer: B
Comments