top of page
  • Writer's picturekeshprad

PhysicsBowl 2018 Q40


40) For this question, we want to find the wavelength that produces the lowest kinetic energy during Einstein's photoelectric effect. This means that if we solve for the wavelength when the kinetic energy is zero, the correct answer choice will be the wavelength that is closest to this.


The max kinetic energy of the photoelectrons can be expressed with the following equation. Using Planck's formula for the energy of a photon and the general wave function, we can bring this in terms of the wavelength.

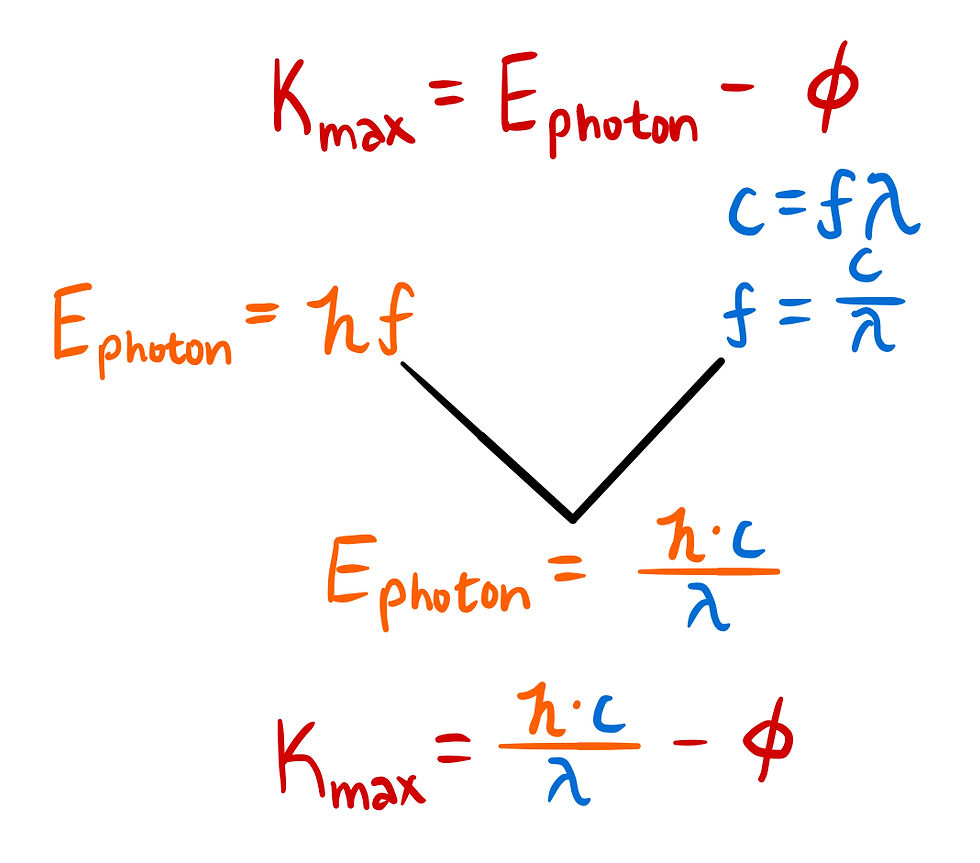
Where K is kinetic energy, E is energy of the photon, ϕ is the work function, h is Planck's constant, f is frequency, c is the speed of light, and λ is wavelength

Remember that at the beginning of the question I mentioned that the wavelength that will produce the lowest kinetic energy will be the answer choice that is closest to wavelength which would keep the kinetic energy at 0.


This means our next step is to assume K[max] to be 0 and solve for λ.

Where K is kinetic energy, ϕ is the work function, h is Planck's constant, f is frequency, c is the speed of light, and λ is wavelength

The problem says that all choices are listed in nanometers, so let's convert our answer as well.

Where λ is wavelength

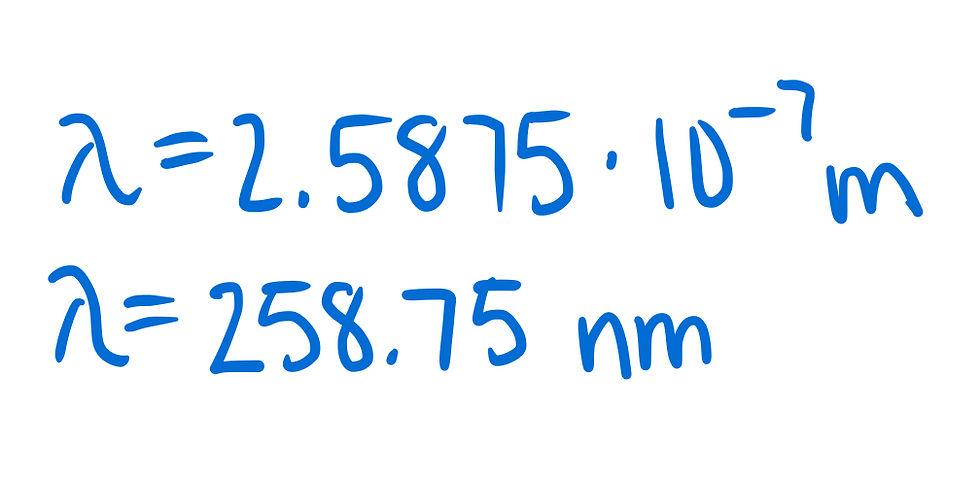
Finally, as thoroughly explained above, we will choose the answer choice closest to this.


Answer: C

Comments

bottom of page