PhysicsBowl 2019 Q30

PhysicsBowl Home Page

PhysicsBowl 2019

30) This question asks us to find the linear speed of a wheel after it is accelerated by a torque applied for 4 seconds. For this question, it will be easiest to set up the impulse-momentum theorem relation for angular motion.

Where τ is torque, t is time, L is angular momentum, I is rotational inertia, and ω is angular velocity

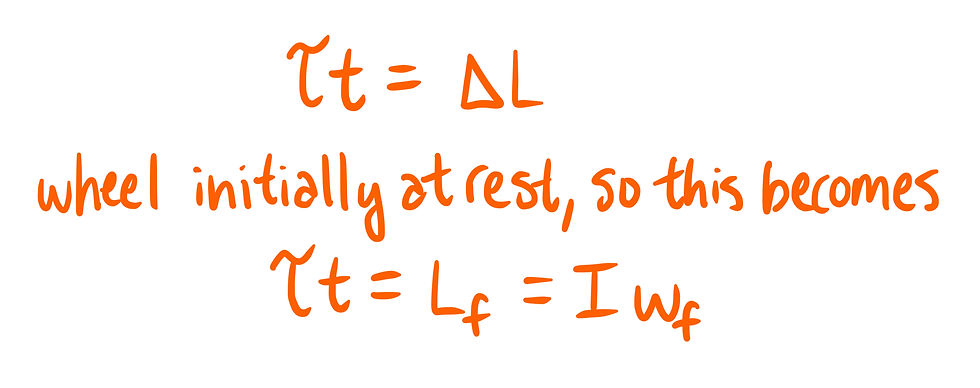
After this, we need to replace torque(τ), rotational inertia(I) and angular velocity(ω). Using angular to translational motion equations we can simplify τ and ω. And by approximating the wheel as a hoop, we can use a predefined formula for the rotational inertia of a hoop rotating about its central axis.

Where F is applied force, r[g] is the radius of the gear, t is time, m[w] is the mass of the wheel, r[w] is the radius of the wheel, and v[w] is the linear velocity of the wheel

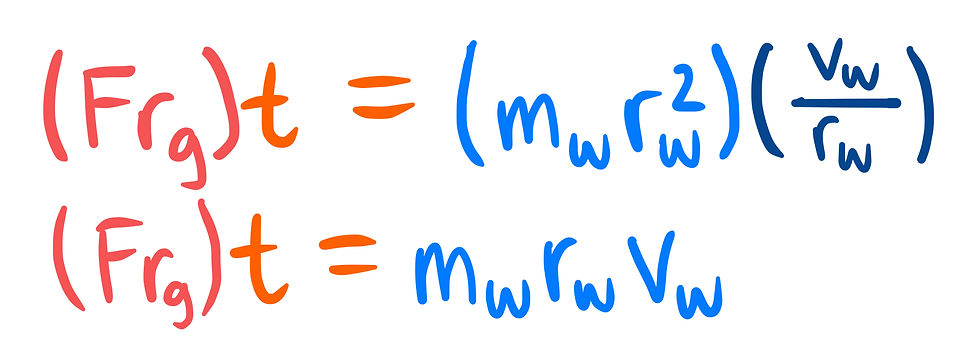
Finally, solving for v[w] and plugging in our given values, we will find our answer.

Where v[w] is linear velocity of the wheel, F is applied force, r[g] is radius of the gear, t is time, m[w] is mass of the wheel, and r[w] is radius of the wheel

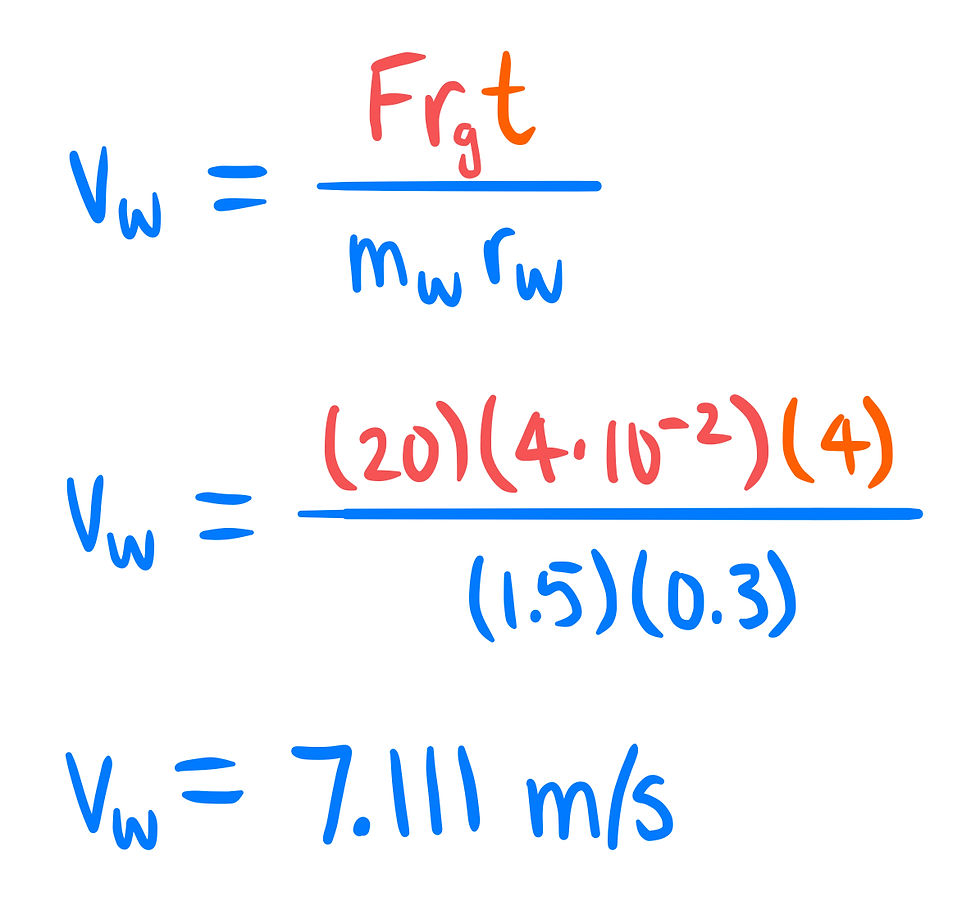
Answer: C