Princeton Review 16th Edition PT1 Q13

Princeton Review's Book

13) This question simulates a man dropping a hammer while standing on the moon. They prompt us to write an expression to find the acceleration due to gravity of the hammer. We should start with our formula for universal gravitational force.

Where Fg is force due to gravity, G is the universal constant of gravity, M1 is the mass of the central object, M2 is the mass of the object being dropped, and r is the distance between the two objects

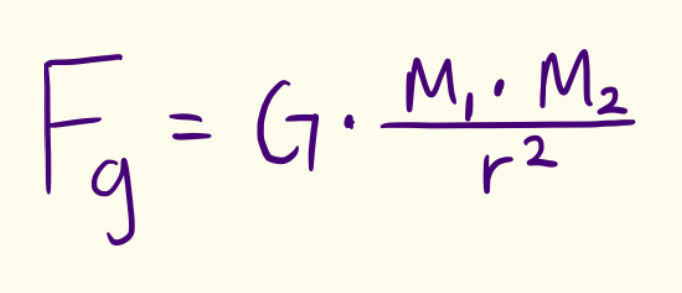
For this case, we will take M1 as the mass of the moon and M2 as the mass of the hammer. If you are interested, the universal constant of gravity can be approximated to 6.67×10^−11. However, for this problem, we do not need to know this value.

Using Newton's 2nd Law, we can also say that Fg = M2(mass of hammer) * a(due to gravity).

Where a is acceleration of the hammer due to gravity on moon

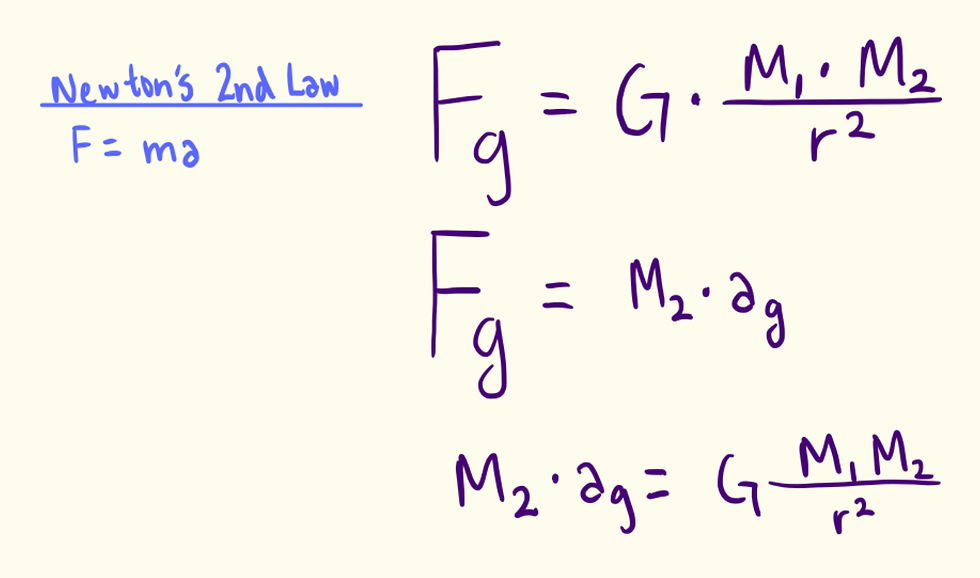
And finally, we can divide both sides by M2, substitute M2 with the given mass of the moon(M), and substitute r with the given distance between the moon and the hammer. We normally want to take the distance from the center of the moon to the center of the hammer. But because of the large size of the moon in comparison to the hammer, we can just use the radius of the moon as an approximation.

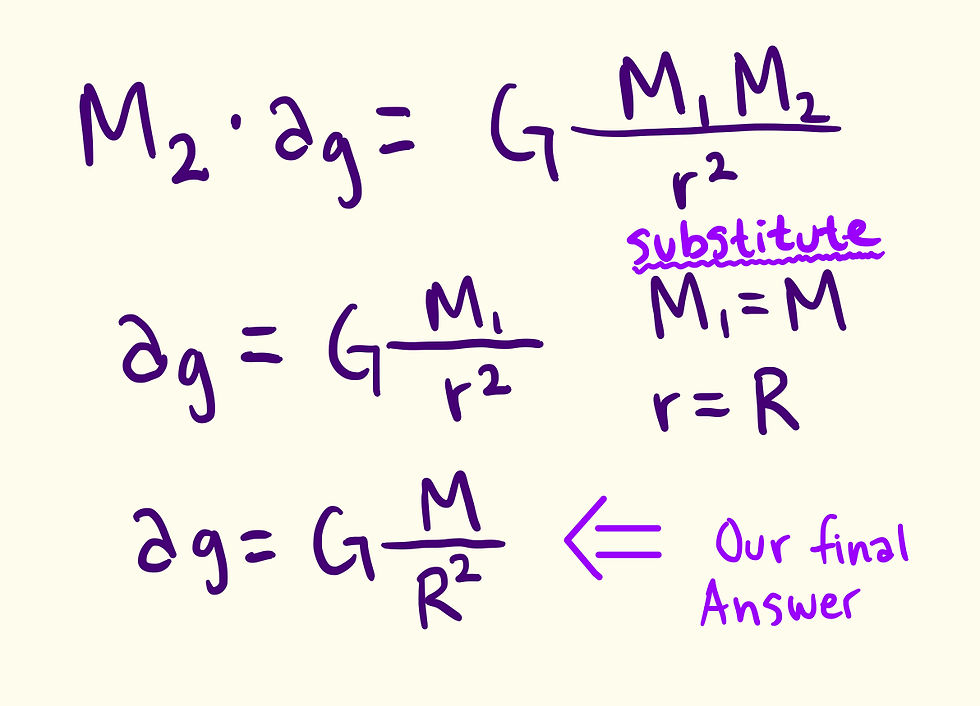
So, our final answer is B.

Answer: B